Agradecimientos

¿Qué son las funciones de distancia con signo?

Las funciones de distancia nos permiten describir figuras geométricas calculando la distancia entre un punto arbitrario y una superficie. Esto significa que podemos modelar figuras geométricas sin vértices y con resolución infinita. Las funciones de distancia permiten describir primitivas y aproximar bastante bien la superficie de estas.

Una de las distancias más fáciles de calcular es la distancia a una esfera. Esta se calcula obteniendo la longitud de la posición de la esfera menos el radio.

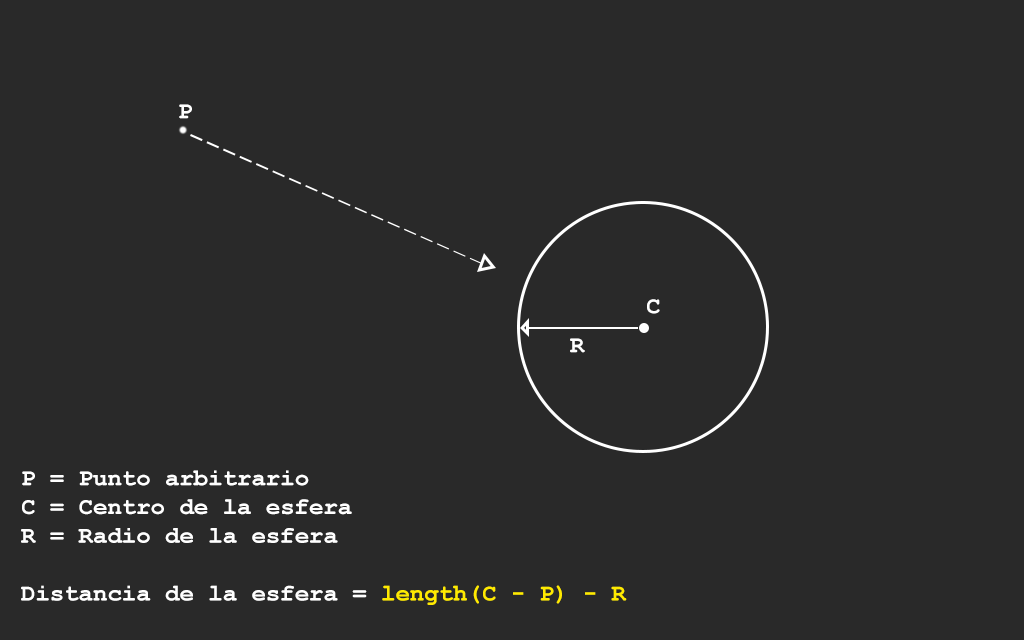
Podemos representarlo en GLSL de esta forma:

float DistanciaAEsfera(vec3 posicionDelRayo, vec3 centro, float radio)
{
    return length(centro - posicionDelRayo) - radio;
}

Esta es una visualización del campo de distancia que la función genera:

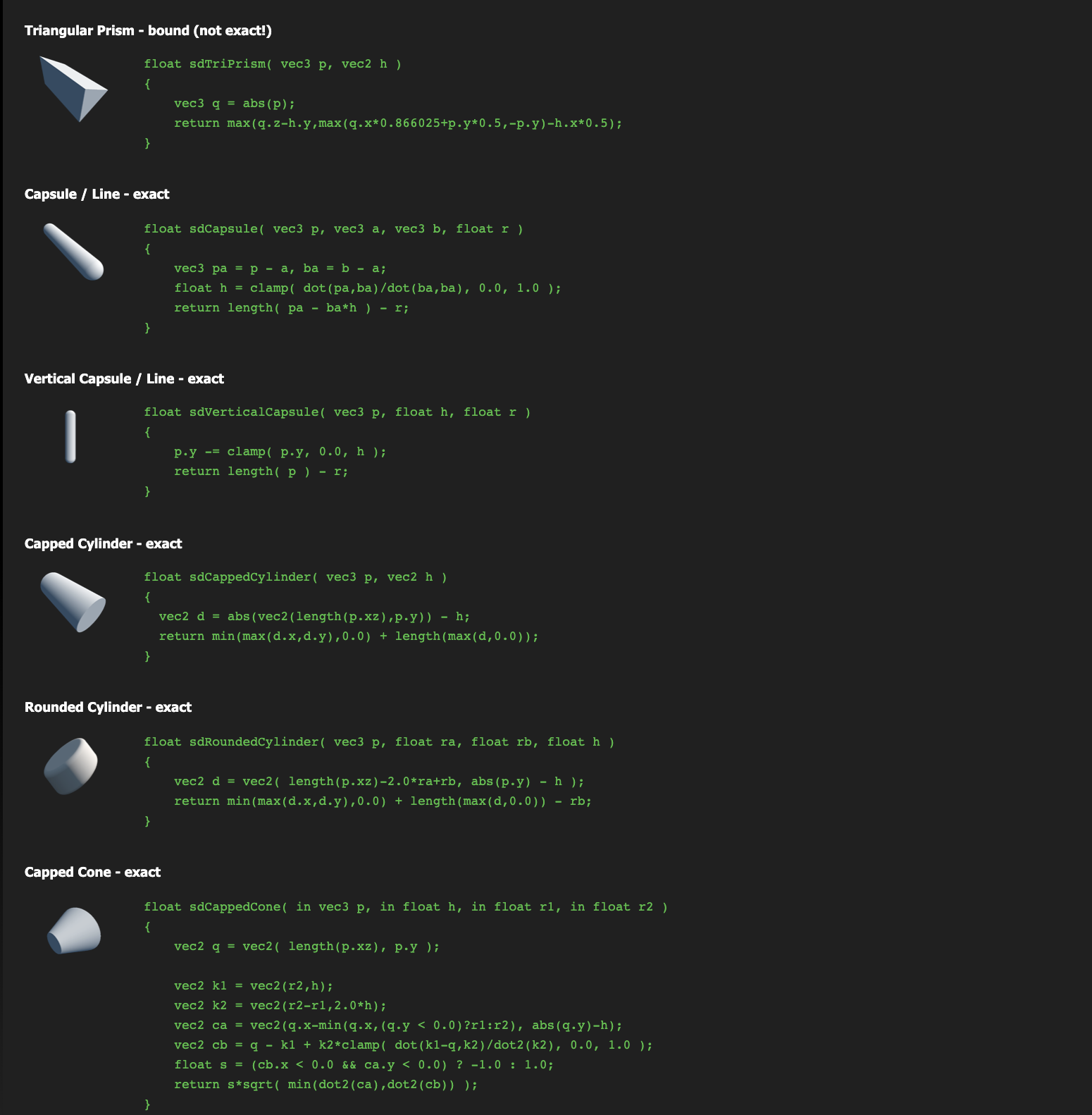
Hay muchas funciones documentadas que pueden ser utilizadas para componer una escena.

Un par de ejemplos de otras funciones:

Cubo

float DistanciaACubo(vec3 posicionDelRayo, vec3 centro, vec3 dimensiones)
{
    vec3 punto = abs(centro - posicionDelRayo) - dimensiones;
    return length(max(punto, 0.0)) + min(max(punto.x, max(punto.y, punto.z)), 0.0);
}

Toro

float DistanciaAToro(vec3 posicionDelRayo, vec3 centro, vec2 radios)
{
    vec3 posicion = centro - posicionDelRayo;
    vec2 t = vec2(length(posicion.xy) - radios.x, posicion.z);
    return length(t) - radios.y;
}

Una de las grandes ventajas que tiene esta técnica es que podemos ocupar operaciones booleanas entre diferentes funciones a un bajo costo.

OR nos permite unir dos volumenes.

float OR(float a, float b)
{
    return min(a, b);
}

NOT resta un volumen de otro.

float NOT(float a, float b)
{
    return max(a, -b);
}

AND nos devuelve la intersección de dos volumenes.

float AND(float a, float b)
{
    return max(a, b);
}

Pueden encontrar muchas más funciones documentadas en la página de Íñigo Quílez.

¿Qué es ray marching?

Ray marching es una técnica, pariente del ray casting, utilizada para dibujar escenas 3D. Consiste en generar rayos desde un punto y marchar por cada uno de ellos en una dirección hasta chocar con un volumen o llegar a una distancia máxima definida por nuestro programa.

Uno de los algoritmos de ray marching más populares es el sphere tracing. Este algoritmo consiste en tomar la distancia más cercana a la escena desde la posición actual del rayo. Luego utilizar esa distancia para dar el siguiente paso en la marcha en dirección del rayo. El proceso se repite hasta que la distancia sea tan corta que podamos decir que hay un choque entre el rayo y la superficie. Este algoritmo nos permite reducir la cantidad de pasos que damos y también mejora la precisión de nuestro rayo al indicar si ha tocado la escena o no.

Acá podemos visualizar el algoritmo:

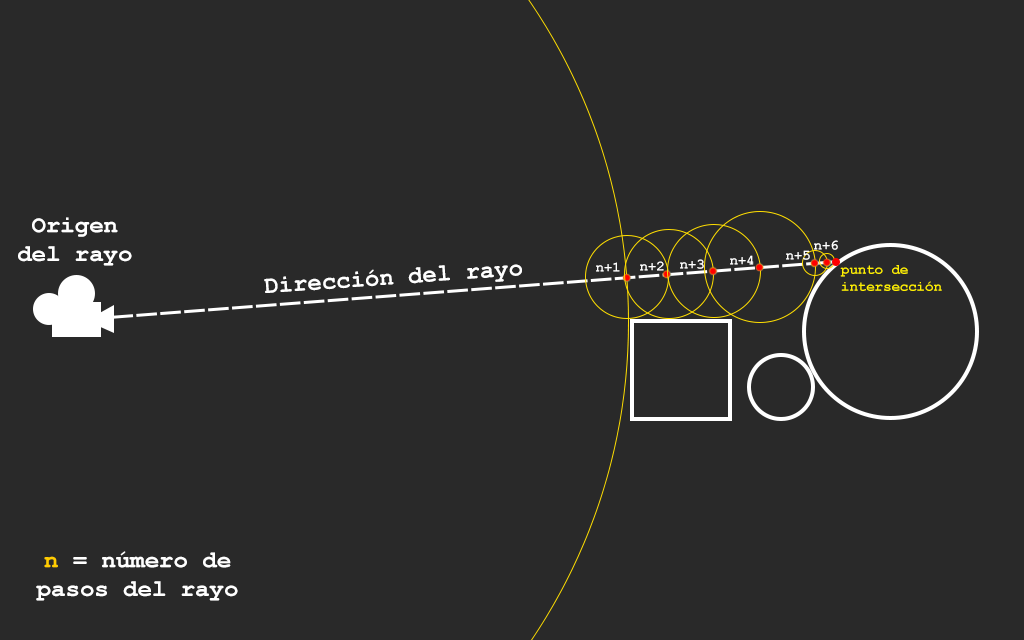
Esta forma de representar volúmenes con funciones y ocupando ray marching ha sido utilizada por varios años dentro del mundo del demoscene para generar escenas con gran variedad, pero manteniendo los ejecutables muy pequeños.

Acá podemos apreciar una demo del 2017 que solo pesa 59.5 KB creado con ray marching y funciones de distancia.

Poo Brain - Eidolon (Revision 2017 64K compo winner)

Otro lugar donde esta técnica es muy popular es en la página web Shadertoy

¿Qué beneficios tiene utilizar ray marching con funciones de distancia?

La mezcla de ray marching y funciones de distancia nos permite renderizar escenas muy difíciles de crear utilizando el pipeline gráfico tradicional. Por ejemplo, poder mezclar diferentes volúmenes dinámicamente, tener efectos volumétricos como humo o nubes, calcular fácilmente sombras suaves u oclusión ambiental, subsurface scattering, entre otras cosas.

Sin embargo, hay que entender que esta técnica no es un remplazo a pipeline tradicional, es más bien una herramienta que permite resolver problemas específicos.

¿Cómo implementamos un ray marcher?

float distanciaTotal = 0.0;
vec3 colorDeLaEscena = vec3(0.0);
for (int paso = 0; paso < NUM_PASOS_MAX; ++paso)
{
    vec3 rayo = origenDelRayo + direccionDelRayo * distanciaTotal;
    float dist = DistanciaALaEscena(rayo);

    if (dist < DISTANCIA_MIN)
    {
        colorDeLaEscena = DibujarEscena(rayo);
        break;
    }

    distanciaTotal += dist;

    if (distanciaTotal > DISTANCIA_MAX)
    {
        break;
    }
}
return colorDeLaEscena;

La implementación de un loop de ray marching consiste en solo un par de líneas de código. Dentro de nuestro loop lo primero que hacemos es obtener la distancia desde el punto actual de nuestro rayo hacia la escena.

float dist = DistanciaALaEscena(origenDelRayo + direccionDelRayo * distanciaTotal);

Luego verificamos si la distancia es tan corta que podemos decir que el rayo está en la superficie de nuestra escena.

if (dist < DISTANCIA_MIN)
{
    // Estamos tan cerca del volumen que podemos 
    // decir que nuestro rayo ha colisionado con la escena.
    break;
}

Si no lo está, incrementamos la distancia total recorrida del rayo por la distancia en la que este se encuentra actualmente.

distanciaTotal += dist;

Si esa distancia es superior a la distancia máxima que nosotros definimos, podemos estar seguros de que el rayo no va chocar con ninguna superficie y, por ende, podemos cortar el loop.

if (distanciaTotal > DISTANCIA_MAX)
{
    // Nuestro rayo ha superado la distancia máxima.
    // Para evitar que avance hasta el infinito cortamos el loop.
    break;
}

¿Cómo describimos nuestra escena?

Para describir nuestra escena utilizaremos funciones de distancia como las que mencioné anteriormente.

La función que describe la escena solo requiere un parámetro, y es la posición actual del rayo que será utilizado para calcular la distancia hacia los volúmenes que componen la escena.

float DistanciaALaEscena(vec3 posicionDelRayo)
{
    float cubo = DistanciaACubo(posicionDelRayo, vec3(-2.0, 0.0, 0.0), vec3(2.0));
    float esfera = DistanciaAEsfera(posicionDelRayo, vec3(2.0, 0.0, 0.0), 2.5);
    return OR(esfera, cubo);
}

En esta función definimos la distancia a nuestra escena. Describimos un cubo y una esfera, los unimos utilizando la operación booleana OR.

Si renderizamos esta escena utilizando la distancia total de cada rayo, se ve así:

¿Cómo podemos iluminar nuestra escena?

Para poder iluminar una escena 3D primero debemos tener el vector normal de nuestra superficie. En el pipeline tradicional, por lo general, este vector ya viene calculado y forma parte de la estructura del vértice. Como nosotros componemos nuestra escena sin vértices, debemos encontrar otra forma de obtener este vector.

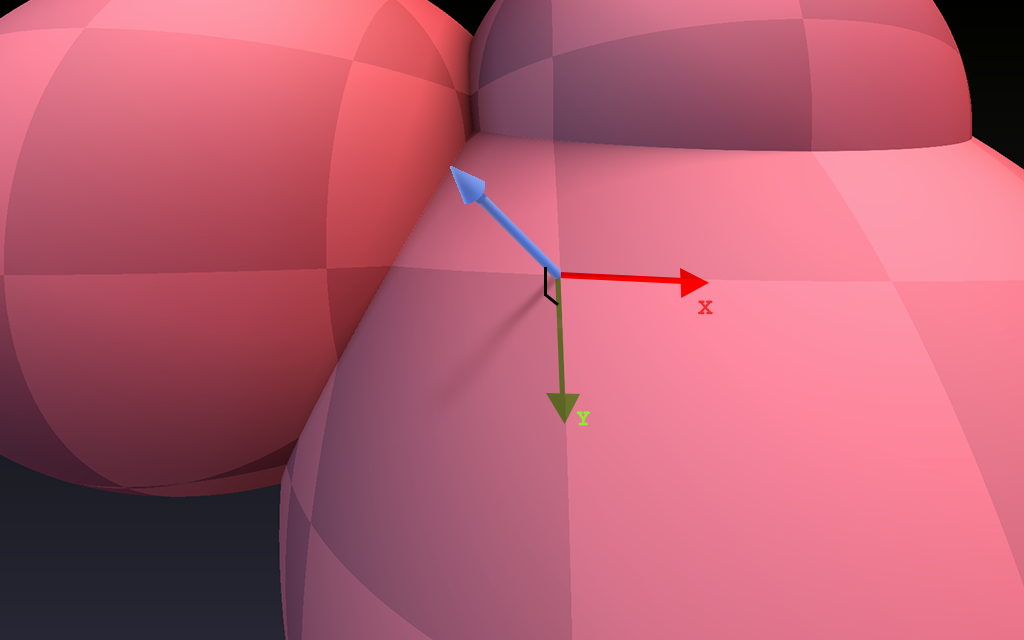
En el caso de las funciones de distancia lo que haremos es tomar varias muestras de distancia al rededor de nuestro punto de intersección y luego calcularemos la diferencia central. Esto nos devolverá el gradiente de la superficie en el punto actual en que el rayo choca. Este gradiente es perpendicular a la superficie por lo cual se alinearía con la dirección del vector normal.

La función para calcular la normal se ve así:

vec3 VectorNormal(vec3 punto)
{
    const float epsilon = 0.0001;
    const vec2 E = vec2(0.0, epsilon);
    return normalize(vec3(
        DistanciaALaEscena(punto + E.yxx) - DistanciaALaEscena(punto - E.yxx),
        DistanciaALaEscena(punto + E.xyx) - DistanciaALaEscena(punto - E.xyx),
        DistanciaALaEscena(punto + E.xxy) - DistanciaALaEscena(punto - E.xxy)
    ));
}

Si visualizamos el resultado, podemos ver el vector normal de la superficie pintado en la pantalla.

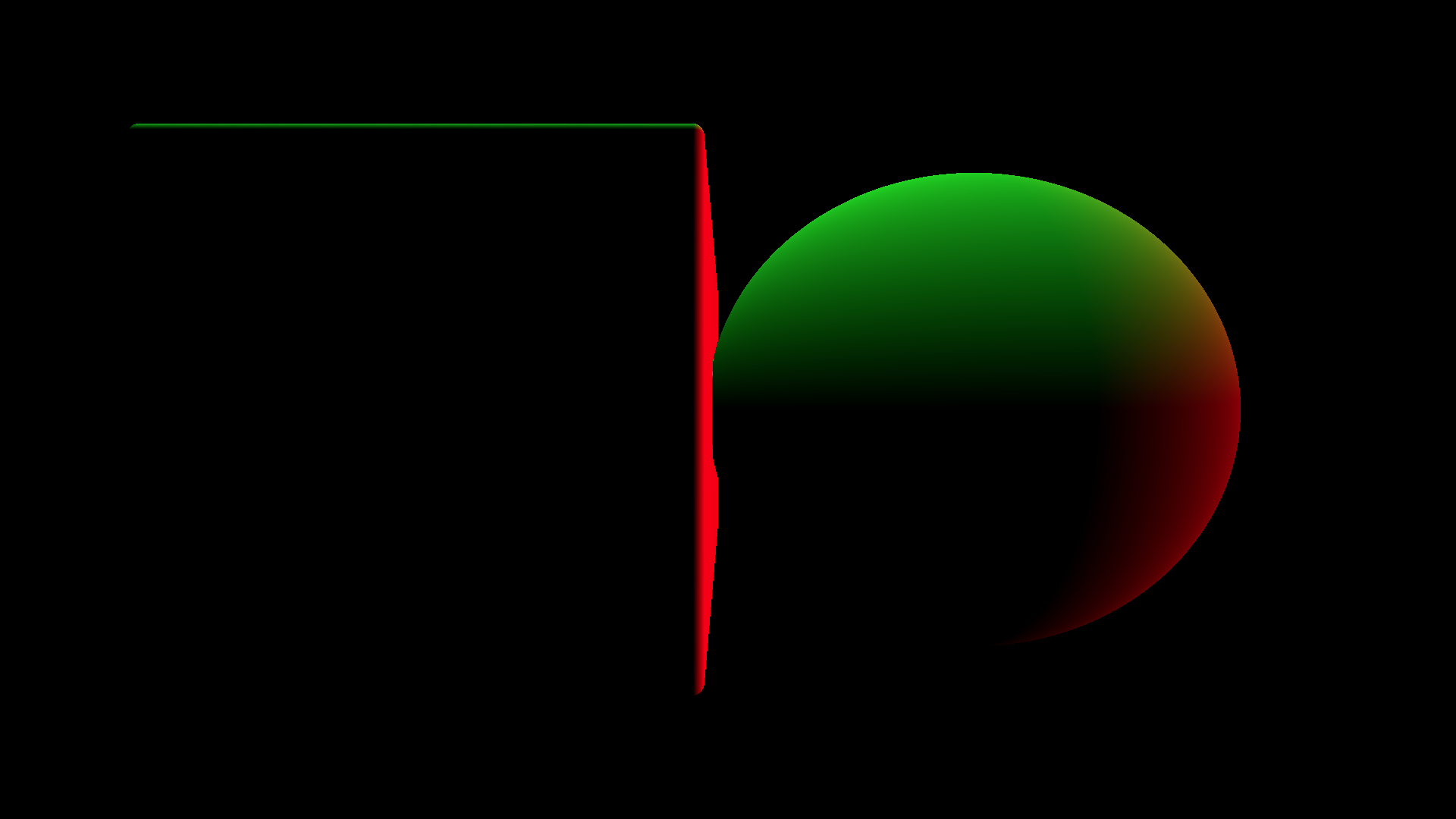
Ya teniendo nuestro vector normal, podemos implementar cualquier modelo de iluminación que utiliza este vector.

En nuestro caso una simple luz direccional difusa hace que resalte inmediatamente las figuras.

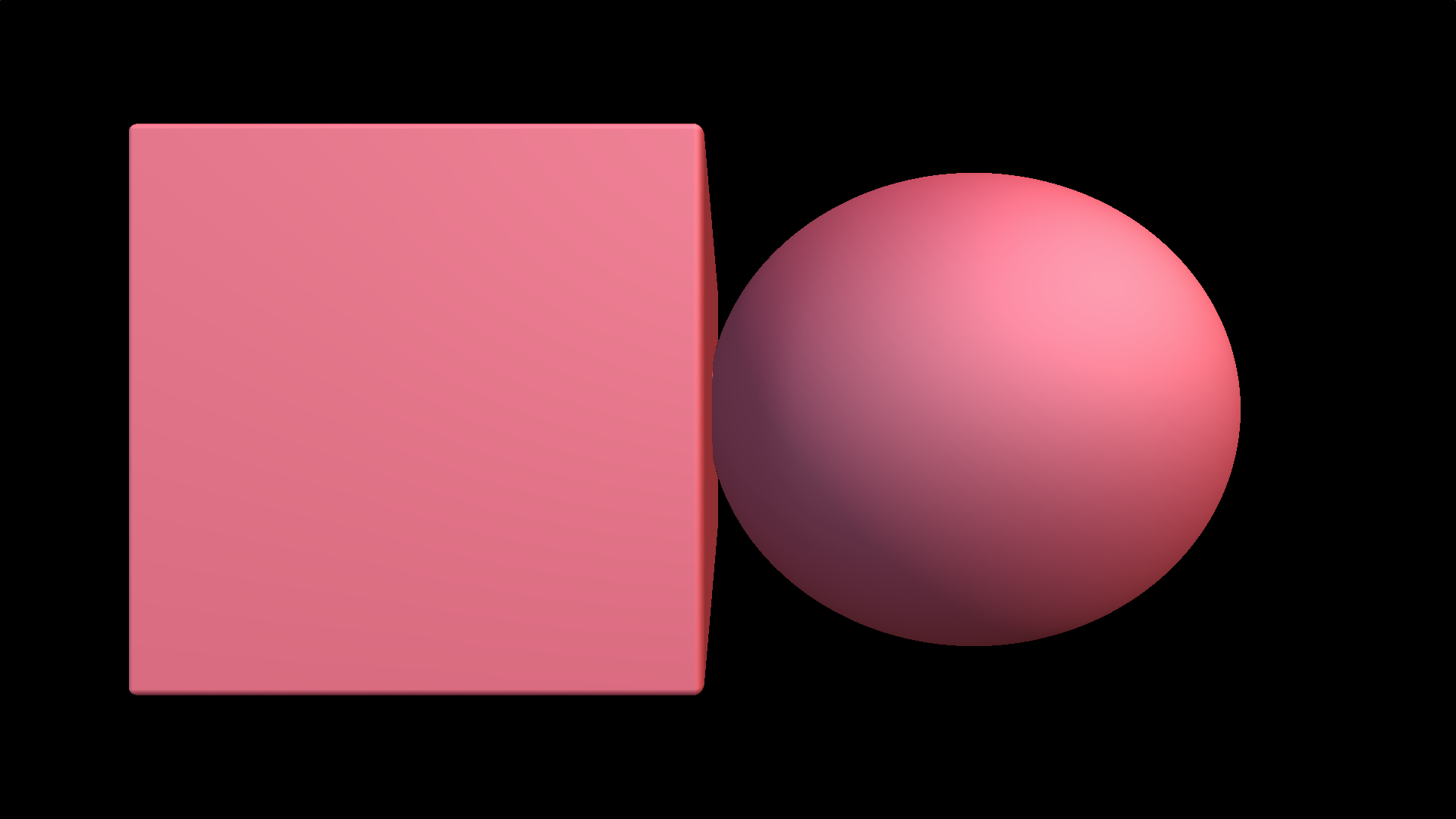
¿Cómo implementar sombras?

Una de las ventajas que mencioné al comienzo sobre utilizar funciones de distancia con ray marching es que facilitaba bastante calcular efectos que suelen ser más complejos en el pipeline tradicional. Por ejemplo, las sombras suaves.

Las sombras en el pipeline tradicional se suelen implementar utilizando shadow mapping. Esta técnica consiste en dibujar la escena desde el punto de vista de la luz y luego ocupar el depth buffer de esa captura para saber qué partes de la escena están ocluidas por otros objetos. Un problema que tiene esta técnica es que suele producir errores visuales si no hay cuidado.

Uno de los más comunes que pueden ser visibles con shadow mapping es el que se conoce como shadow acne. Un ejemplo de eso es visible en la siguiente imagen.

Lo más probable es que la gente que ha trabajado con motores populares y utilizado shadow mapping ha tenido que ajustar algunos parámetros para poder evitar el shadow acne.

Con ray marching y funciones de distancia podemos calcular fácilmente si es que la superficie está ocluida en el punto actual. Lo único que hay que hacer es marchar nuevamente desde el punto donde nuestro rayo chocó con el volumen en la dirección de la luz. Si la distancia es menor a la distancia máxima, entonces nuestra superficie está ocluida, por ende, dibujamos una sombra.

float CalcularSombra(vec3 posicionDelRayo, vec3 direccionDeLaLuz)
{
    float distanciaTotal = 0.01;
    for (int i = 0; i < 100; ++i)
    {
        vec3 rayo = posicionDelRayo + direccionDeLaLuz * distanciaTotal;
        float distanciaActual = DistanciaALaEscena(rayo);
        if (d < 0.0001) return 0.2;
        distanciaTotal += distanciaActual;
        if (t > 100.0) break;
    }
    return 1.0;
}

Esto nos permite tener sombras duras, tal como se ve en la imagen:

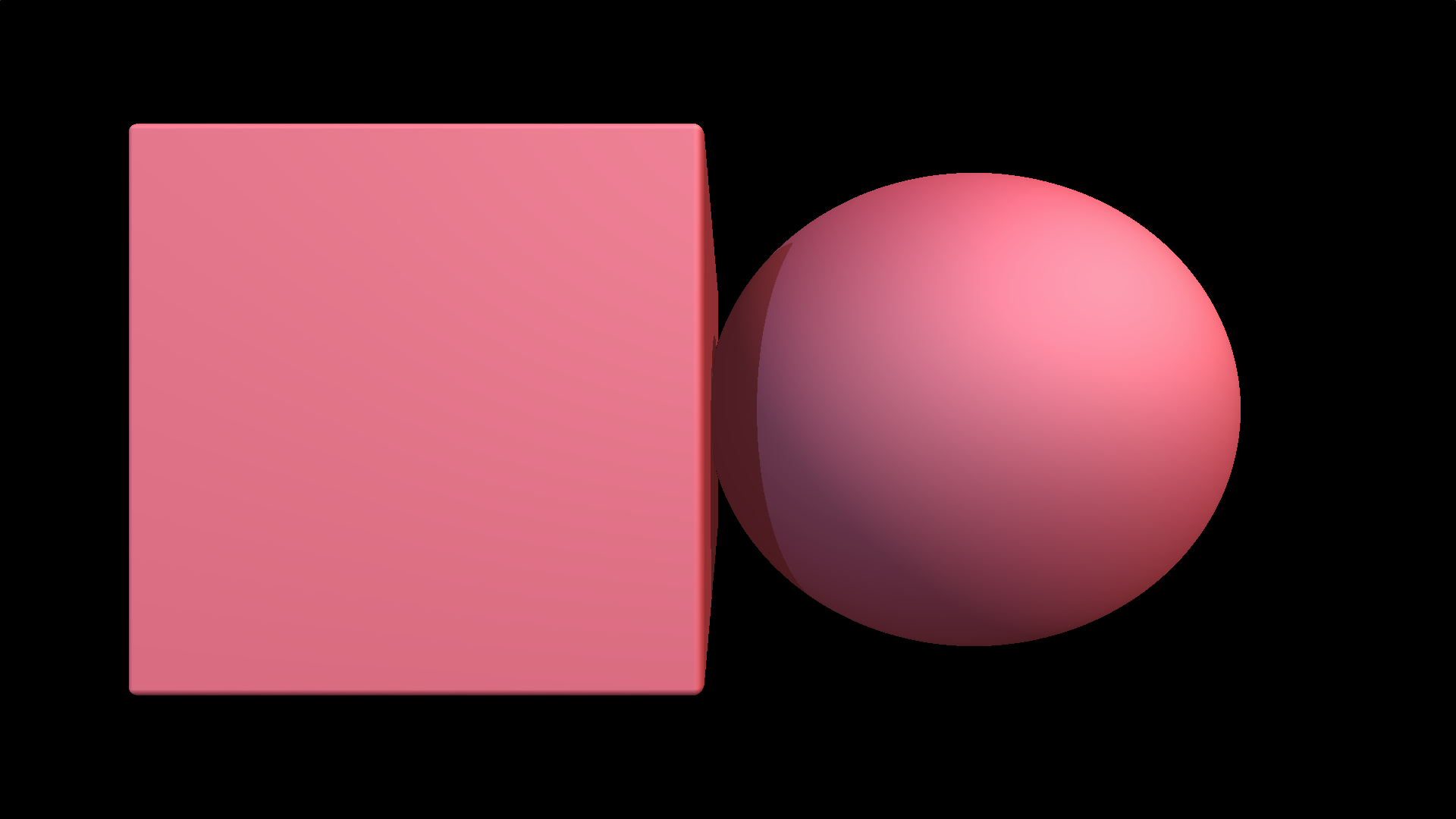
Solo con hacer unos pequeños cambios a esta función podemos obtener sombras suaves.

float CalcularSombra(vec3 posicionDelRayo, vec3 direccionDeLaLuz)
{
    float sombra = 1.0;
    float distanciaTotal = 0.1;
    for (int i = 0; i < 32; ++i)
    {
        vec3 rayo = posicionDelRayo + direccionDeLaLuz * distanciaTotal;
        float distanciaActual = DistanciaALaEscena(rayo);
        sombra = min(sombra, distanciaActual / distanciaTotal);
        distanciaTotal += clamp(d, 0.0, 0.6);
    }
    return clamp(sombra * 2.0, 0.0, 1.0);
}

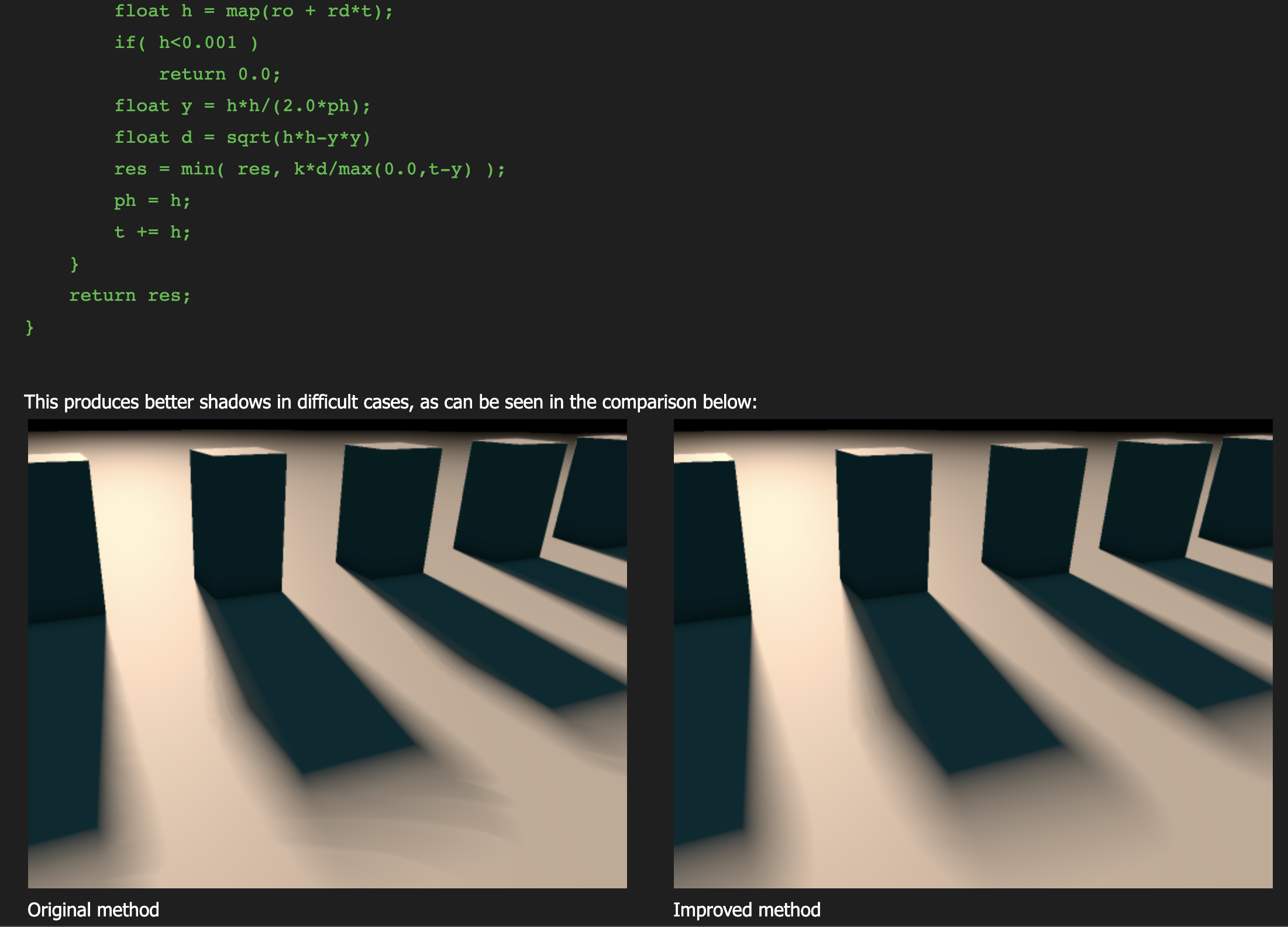
Si en vez de devolver un valor fijo dividimos la distancia de la escena por la distancia total en cada paso de nuestro rayo y guardamos el mínimo, obtenemos un degradado el cual produce el efecto de sombra suave. Esto surge porque utilizamos la misma distancia al objeto que ocluye nuestra superficie para generar una penumbra

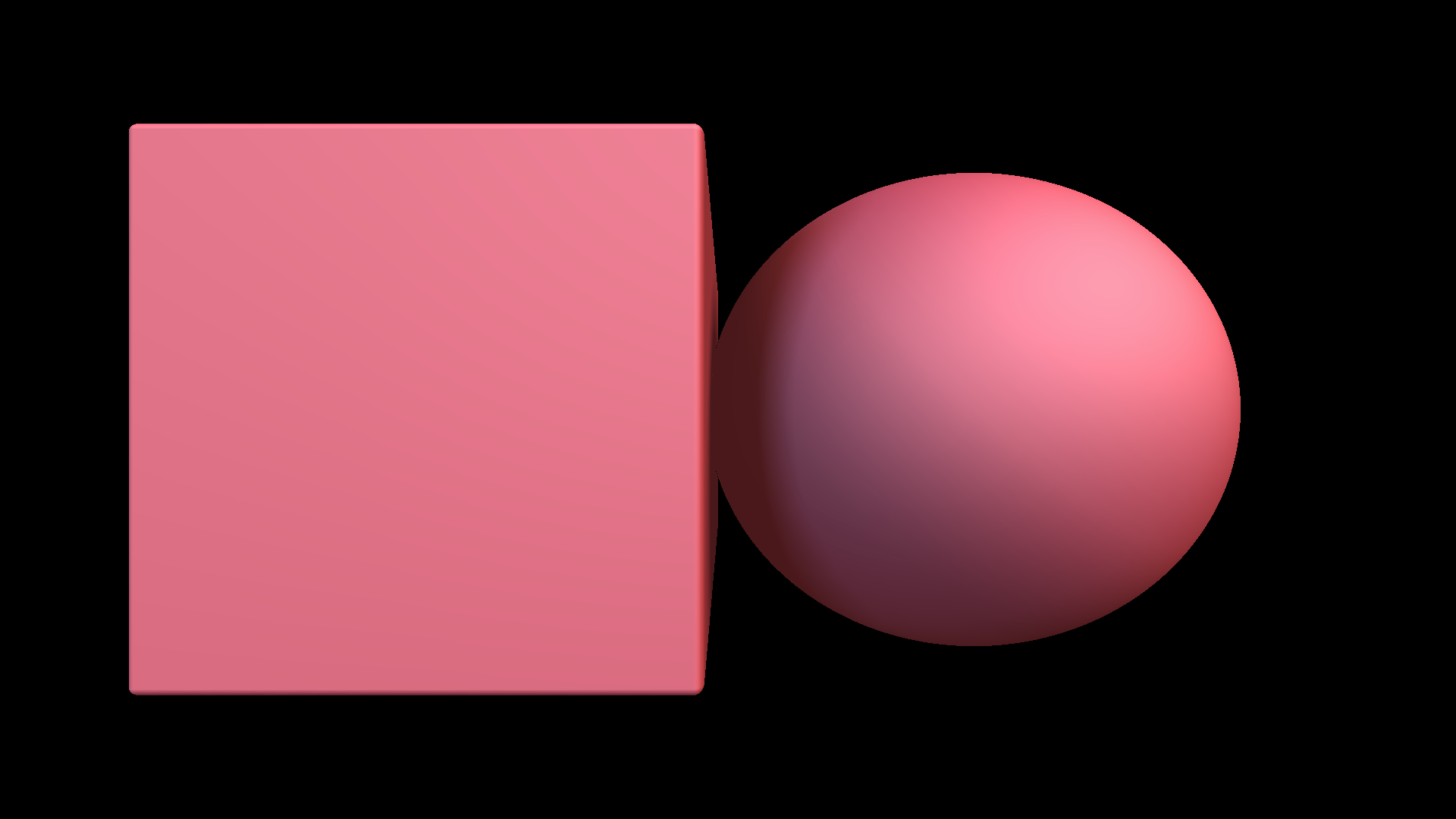
Esta función produce resultados bastante buenos y realistas, como se puede ver en esta escena un poco más compleja.

Existen varias soluciones documentadas para calcular sombras suaves con ray marching. Un buen ejemplo de implementación puede ser encontrado en el blog de Iñigo Quílez.

¿Cómo implementar reflejos?

Otra de las técnicas que se vuelven bastante fáciles de calcular son los reflejos. Al igual que la anterior, es complicada de lograrla correctamente en el pipeline tradicional. En el que, por lo general, se utilizan diferentes técnicas para lograr un reflejo perfecto, como, por ejemplo, SSR, cubemaps, entre otros. Lo único que hay que hacer es reflejar la dirección del rayo por el vector normal de la superficie. Luego iterar por cada rebote de luz que uno quiera hacer.

En este ejemplo solo hago dos rebotes de luz y ya podemos notar una gran diferencia en fidelidad:

El código de esto se ve así:

for (int rebote = 0; rebote < NUM_REBOTES_MAX; ++rebote)
{
    float distanciaTotal = 0.0;

    for (int paso = 0; paso < NUM_PASOS_MAX; ++paso)
    {
        float dist = DistanciaALaEscena(origenDelRayo + direccionDelRayo * distanciaTotal);

        if (dist < DISTANCIA_MIN)
        {
            // Estamos tan cerca del volumen que podemos 
            // decir que nuestro rayo ha colisionado con la escena.

            vec3 posicionDelRayo = origenDelRayo + direccionDelRayo * distanciaTotal;
            vec3 normal = VectorNormal(posicionDelRayo);

            // Acumulamos la luz y reflejamos nuestra dirección del rayo.

            direccionDelRayo = normalize(reflect(direccionDelRayo, normal));
            origenDelRayo = posicionDelRayo + direccionDelRayo * 0.01;

            break;
        }

        distanciaTotal += dist;

        if (distanciaTotal > DISTANCIA_MAX)
        {
            // Nuestro rayo ha superado la distancia máxima.
            // Para evitar que avance hasta el infinito cortamos el loop.
            break;
        }
    }
}

Lo que hicimos acá fue colocar nuestro loop de ray marching dentro de otro loop de rebote de rayos y por cada iteración de ray marching acumulamos la luz reflejada de la superficie. Esto produce el efecto de reflejo que vemos en la imagen.

¿Cómo interpolar entre diferentes volumenes?

Otra gran ventaja que tiene ray marching con funciones de distancia es que podemos fácilmente interpolar dos volúmenes utilizando interpolación lineal. Esto nos permite tener un efecto que no es trivial de lograr en el pipeline tradicional.

En GLSL podemos utilizar la función mix. Esta interpola linealmente.

float DistanciaALaEscena(posicionDelRayo)
{
    float escenaA = DistanciaALaEscenaA(posicionDelRayo);
    float escenaB = DistanciaALaEscenaB(posicionDelRayo);

    return mix(escenaA, escenaB, abs(sin(tiempo)));
}

Aquí estamos utilizando el seno del tiempo para animar una interpolación entre dos escenas.

El resultado se ve así:

Ejemplos en produccion

Una técnica utilizada en producción es transformar geometría modelada con vértices a campos de distancia guardados en texturas volumétricas. Un ejemplo es Unreal Engine 4 que utiliza este método para poder generar sombras suaves y oclusión ambiental en tiempo real. UE4 lo llama Mesh Distance Fields.

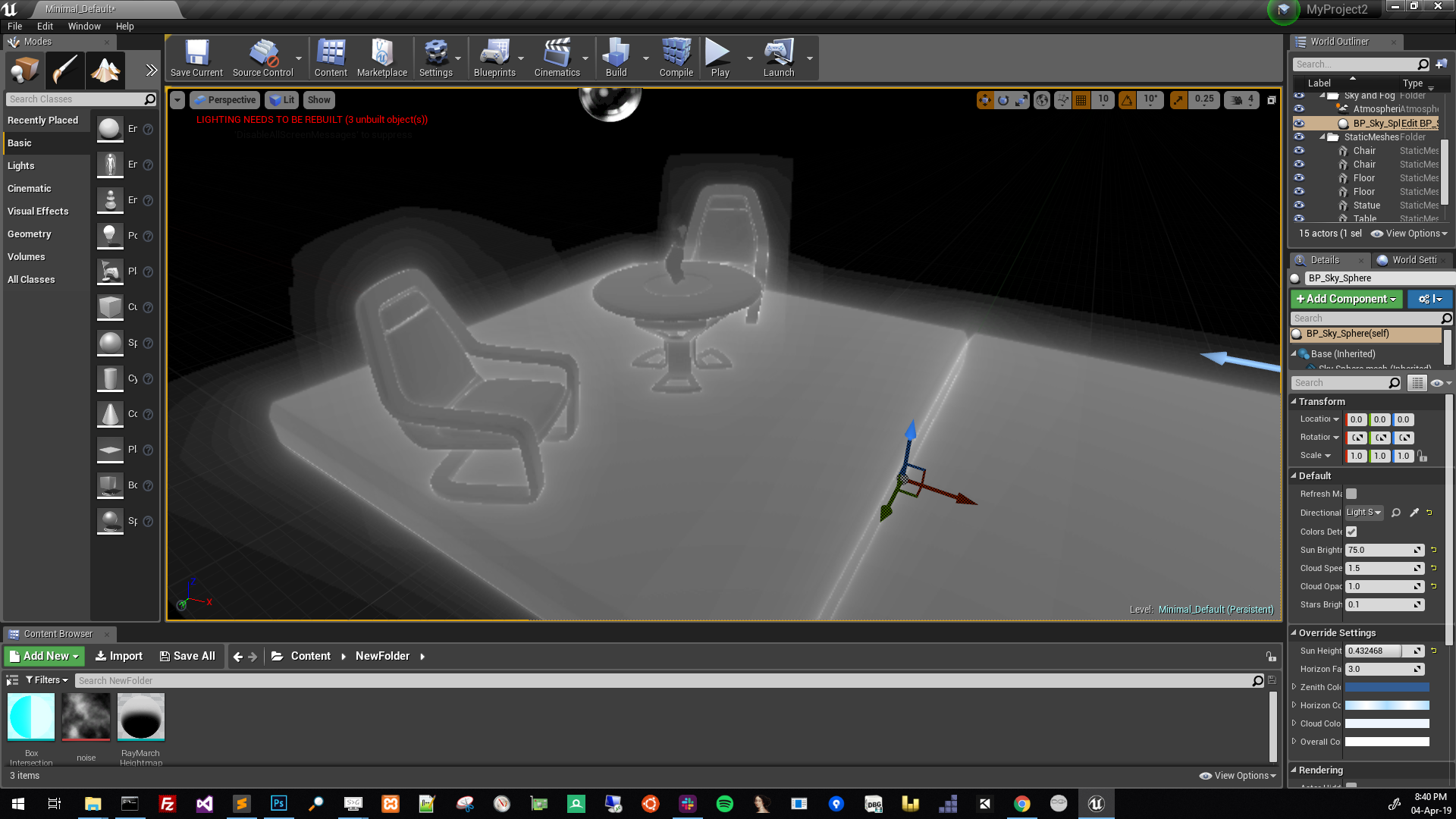
Estas texturas son generadas offline, por lo cual, son útiles solo en cierto tipo de casos. Tiene otro tipo de límites, como el tamaño de las texturas volumétricas. Mientras más detalle uno quiera, más memoria ocupa. Por ejemplo, la textura volumétrica de la silla de la imagen pesa alrededor de 8 MB.

Juegos

Dos juegos que utilizan ray marching con campos de distancia generados en tiempo real y que tienen resultados visualmente hermosos son Dreams por MediaMolecule y Claybook por Second Order.

Dreams por MediaMolecule

Claybook por Second Order

Ambos juegos son un excelente ejemplo del uso de esta técnica, ya que entregan libertad creativa para deformar el mundo.

Punto Final

Espero que después de escuchar esta presentación se motiven a explorar ray marching con funciones de distancia. Que, por ejemplo, se unan a Shadertoy y comiencen a explorar e investigar los shaders que otras personas programan. Personalmente me gusta mucho crear escenas solo con funciones porque entregan gran versatilidad y flexibilidad creativa. Acá solo mostré un poco de lo que se puede hacer, hay muchos más efectos que se pueden lograr con esta técnica, como, por ejemplo, subsurface scattering, oclusión ambiental, refracción, volúmenes con opacidad, etc.

Shadertoy

https://www.shadertoy.com/

Lista de funciones de distancia

https://iquilezles.org/www/articles/distfunctions/distfunctions.htm

Workshop de Ray Marching

http://hughsk.io/fragment-foundry/

Shaders

Logo de Game Dev Planet 3D

https://www.shadertoy.com/view/3lX3DH

Imágenes de las diapositivas

https://www.shadertoy.com/view/Wd2Xzy

Volumen con opacidad (nube)

https://www.shadertoy.com/view/3dSSDD